점군(포인트 그룹 Point group) 완벽히 이해하기
☆ 포인트 그룹이란?
포인트 그룹(점군, Point group)이란 공통된 symmetry operation을 갖는 입체 형태를 구분하기 쉽게 여러 분류로 묶어서 구분하는 것입니다.
여기서 symmetry operation(대칭 작업)은 어떤 분자의 위치를 바꾸는 일을 하는 것으로, 거울면에 반사시키거나, 축을 중심으로 회전시키거나, 점을 중심으로 반전시키는 것 등이 있습니다. 포인트 그룹을 나눌 때는 symmetry operation을 적용하기 전과 적용한 후의 분자 구조가 같을 때, 그 operation을 만족한다고, 혹은 그 operation을 가진다고 합니다. (※여기서 분자의 구조가 같다는 말은 모양뿐만 아니라 원자의 위치도 같아야 합니다.) 포인트 그룹에 대해 알아보기 전에 우선 symmetry operation의 종류와 그 의미를 살펴보겠습니다.
☆ Symmetry Operation에 대해 알아보자

Identitiy operation (E)
identity operation은 분자에 어떠한 위치도 바꾸지 않은 것으로 모든 분자가 이 작업에 만족합니다. 대표적으로 CHFClBr이 있으며 이 분자는 오직 E 만을 만족합니다.

rotation operation (C_n) (_는 아래첨자를 의미합니다.)
rotation opertation은 어떠한 축을 기준으로 회전시키는 작업입니다. 아래첨자인 n은 360º/n 만큼 회전시키는 것을 의미합니다. 쉽게 말해서 C_2이면 360º 중 반만 회전시키는 것입니다. 벤젠의 경우 cyclohexane과 달리 평면 정육각형입니다. 그렇기 때문에 C_6을 만족하며 당연히 C_2, C_3 또한 만족합니다. 포인트 그룹에서 여러가지 Cn을 만족하는 경우 n이 가장 큰 수를 씁니다. 이는 포인트 그룹에서 다시 설명하겠습니다.

reflection operation (σ, sigma)
reflection operation은 어떠한 거울상(mirror plane)을 기준으로 그 분자를 반전시키는 작업입니다. 평면 구조의 분자는 그 평면을 거울면으로 삼는 reflection이 항상 있습니다. 예를들면 물과 벤젠 모두 평면 구조이기 때문에 그 평면을 포함하는 거울상이 하나씩 있으며, 물은 2개의 거울상, 벤젠은 각 꼭짓점과 변을 기준으로 총 7개의 거울상을 가집니다.

inversion operation (i)
inversion operation은 어떠한 점(inversion center)을 기준으로 분자를 반전시키는 작업입니다. Ferrocene은 철 원자에 두개의 cyclopentadienyl이 리간드로 있는 착화합물입니다. 그림과 같이 Fe를 중심으로 분자를 반전시키면 전후가 같음을 알 수 있습니다. 가장 쉬운 다른 예로는 이산화탄소가 있습니다. (O=C=O, C를 기준으로)

rotation-reflection operation (S_n)
rotation-reflection operation은 Cn과 σ⊥(Cn 축에 수직하는 거울상)가 합쳐진 작업입니다. 그림으로 설명하자면 ferrocene의 경우 S_10을 만족합니다. S_10 = C_10 x σ⊥ 으로, 360º/10만큼 회전 시킨 후 Fe를 포함하고 회전축에 수직하는 거울상을 기준으로 반전하면 작업 전후가 같음을 알수 있습니다. 가장 쉬운 다른 예로는 methane CH4가 있습니다.
☆ 포인트 그룹 구분하기

위 그림은 포인트 그룹을 완벽히 설명하고 있습니다. 단계별로 어떤 operation을 만족하는지 차례차례 확인하며 분자의 포인트 그룹을 구분하면 쉽게 이해할 수 있습니다.
1. point group of low or high symmetry
말은 어렵게 보이나 그 의미는 아주 쉽습니다. 포인트 그룹을 구분하기 전, 우선적으로 만족하는 포인트 그룹이 있는지 확인해야 합니다. 그 분자의 특징만 보면 대표하는 포인트 그룹의 특성도 파악할 수 있습니다.
[low symmetry]

C_1
회전을 360º/1 만큼, 즉 아무 조작도 가하지 않는 E만을 만족하는 그룹입니다. 위에서 E에 대해 설명할때 쓰인 CHClBr이 대표적입니다.

C_s
오직 하나의 거울상, reflection operation σ 을 가지는 그룹입니다. 그림처럼 해당 분자는 평면을 기준으로한 거울상 1개만 가집니다.
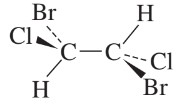
C_i
오직 하나의 점대칭, inversion operation i 을 가지는 그룹입니다. 그림처럼 가운데 탄소 결합의 중심을 inversion center로 가지는 점대칭 1개만 가집니다.
[high symmetry]
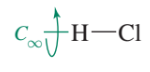
C_∞v
하나의 축을 기준으로 무한히 회전시키는 operation을 가지는 그룹입니다. 대부분의 직선 분자(linear molecule)가 만족합니다.

D_ ∞h
하나의 축을 기준으로 무한히 회전시키고 그 축에 수직하는 C_2를 가지는 그룹입니다. 직선 분자의 한 가운데에 거울상이 있다고 생각하시면 쉽습니다.

T_d, O_h, I_h
분자의 입체 모양에 따라 구분되는 그룹입니다.
T_d는 tetrahedral(정사면체), O_h는 octahedral(정팔면체), I_h는 icosahedral(정이십면체)를 나타냅니다.
다음 그림인 methane의 경우 정사면체 구조를 가지며 T_d를 만족합니다.
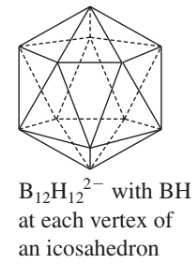
다음 그림은 B12H12^2- (^는 위첨자를 의미합니다.)로 정이십면체 구조를 가지며 I_h를 만족합니다.
하나 주의해야할 점은 각 꼭짓점의 모든 원소가 동일해야합니다. 예를 들어 methane(CH4)의 수소 중 하나가 F, 플루오린으로 바뀐다면(CH3F) 사면체의 구조를 가지지만 모든 꼭짓점의 원소가 같지 않으므로 CH3F는 T_d가 아닌 뒤에서 설명할 C_3 포인트 그룹에 속하게 됩니다.
2. highest-order ratation operation
highest-order rotation operation은 그 분자에서 만족하는 n이 가장 높은 C_n을 확인하는 것입니다.

예를들어 다음 그림의 암모니아의 경우 질소를 기준으로 C_3의 rotation operation을 가집니다.
위에서 1번의 low/high symmetry를 확인하는 이유가 이것인데, 이 포인트 그룹을 만족하지 않는 분자는 무조건 하나 이상의 rotation operation을 가지게 됩니다.
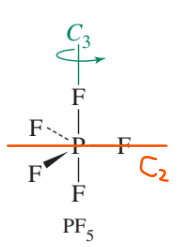
다음으로 highest-order rotation operation의 예를 살펴보자면,
다음 그림에서 확인할 수 있듯이, PF5는 초록색 선을 주축으로 하는 C_3 말고도, 빨간색 선을 주축으로 하는 C_2 또한 있습니다.
하지만 여기서 n이 가장 큰 rotation operation을 확인하기로 했으므로 우리는 C_3를 highest-order rotation operation으로 정합니다.
3. perpendicular C_2 axes?
perpendicular C_2 axes는 2번에서 정한 highest-order 회전 작업의 주축에 대해 수직하는(perpendicular) C_2가 있는지 확인하는 것입니다. 간단한 예와 함께 설명하겠습니다.

이 그림은 바로 위에서 확인한 분자로 highest-order 회전 작업인 C_3의 주축(초록선)에 수직하는 C_2(빨간선)이 있습니다.
이렇게 주축에 수직한 C_2가 있다면 D 그룹으로 나뉘고,
주축에 수직한 C_2가 없다면 C 그룹으로 나뉩니다.
4. horizontal mirror plane(σ_h)
horizontal은 수평이란 뜻이지만, highest-order 회전 작업의 주축에 수직하는 거울상이 있는지 확인합니다.

다시 이 분자를 예로 들면, 주축인 초록선에 수직하는 거울상이 있습니다.
빨간선을 포함하는 평면을 거울상으로 하면 생각하기 쉽습니다.
이렇게 주축에 수직한 거울상이 있는 경우 D_nh, C_nh로 포인트 그룹이 결정되고,
주축에 수직한 거울상이 없는 겅우는 5번으로 넘어갑니다.
PF5는 주축에 수직한 C_2가 있고, 주축에 수직하는 거울상이 있으므로 D_3h 그룹입니다.
물론 5번에서 확인할 주축을 포함하는 거울상도 있지만 순서대로 포인트 그룹을 매깁니다.
5. vertical mirror plane(σ_v, σ_d)
vertical은 수직이란 뜻이지만, highest-order 회전 작업의 주축에 평행(혹은 포함)하는 거울상이 있는지 확인합니다.

NH3의 경우 4번인 σ_h가 없습니다.
거울상은 다음 그림과 같이 총 3개가 있으며 모두 주축인 N을 통과하는 C_3 작업의 주축을 포함하고 있습니다.
이렇게 주축을 포함하는 거울상이 있는 경우 D_nd, C_nv로 포인트 그룹이 결정되고,
주축을 포함하는 거울상이 없는 경우 D_n 그룹이 결정됩니다.
C_n 그룹의 경우 6번으로 넘어갑니다.
NH3는 N을 통과하는 주축인 C_3가 있고, 주축에 수직하는 C_2가 없으며, 주축에 수직하는 거울상이 없고, 주축을 포함하는 거울상이 있으므로 C_3v입니다.
6. rotation-reflection operation(S_n)
rotation-reflection operation이 있는지 확인합니다.

그림의 분자의 경우 주축이 C_2이고 입체 모양을 자세히 살펴보면 주축에 수직하거나 평행한 거울상이 없습니다. (조금 어려울수도 있으나 해당 분자를 직접 그려보면 쉽게 이해됩니다.)
여기서 살펴볼 S_n은 highest-order 회전 작업의 주축을 공유하고 n값이 2배인 것입니다.
그림에선 C_2가 highest-order 회전 작업이므로 주축이 같은 S_4가 있는지 찾아보면 됩니다.
다시 짚어보자면 S_4는 C_4를 한 이후에 σ⊥(Cn 축에 수직하는 거울상)를 하는 것입니다.
S_n이 있다면 S_n으로 포인트 그룹이 결정되고
S_n이 없다면 C_n으로 포인트 그룹이 결정됩니다.
※ low, high symmetry 구분하는 팁
low, high symmetry는 제일 먼저 구분해야하는 포인트 그룹으로 막상 어떤 분자를 보고 무슨 그룹인지 바로 떠올리기는 쉽지 않습니다.
정사면체, 정팔면체와 같이 한눈에 보기 쉬운 것들을 먼저 제외하고,
우선 2번인 분자의 C_n이 있는지 확인합니다. 만약 없다면 C_1(E), C_s(거울상), C_i(점대칭) 중 하나에 속하는 분자입니다.
저는 보통 거울상 - 점대칭 순으로 확인합니다.
C_n을 찾았는데 선형 분자라서 C_∞의 highest-order 회전 작업을 가진다면
3번인 주축에 수직하는 C_2가 있는지 찾아보면 됩니다. 있다면 D_∞v이고, 없다면 C_∞h입니다.
분자가 선형이기 때문에 자동으로 5번의 주축을 포함하는 거울상이 반드시 있습니다.